warning : this very much comes from the view of a computer science student and a math nerd, though I think it aplies to quite a lot of aspects
If you're anything like me you've probably experimented with study methods trying to decide what works best for you. Afterall the idea of spending 3 hours instead of 8 is really appealing. When researching this subject in any capacity you will find a lot of different study methods like mindmapping, summarizing, preperation tests and one that it bassicly praised by everyone I know, flash cards.
All of these methods can learn you a lot about the subject but the main differentiation between most of these is what they focus on.
Flashcards are neat, and they can be very usefull to learn things that you frequently need to recall. But they often lack depth of understanding, after learning a dozen flashcards abotu math formulas you might now them by heart but you don't understand where they came from making you mis out on a lot of opportunities to understand the concepts better. A great example of this was during my calculus class, an insight my professor gave me, we were asked to learn the the formulas for volumes and surfaces of several figures, one of which being the sphere. Which has a rather odd volume formula, namely 4 * pi * r * r, the reason for this throwing people of was due to the surface area formula just being r * r * pi, so the 4 feels almost random.
But the professor explained that by calculating the derivative of the formula for the volume of a sphere u would also get this answer, since we are getting a super small layer of the sphere. Bassicly making the formula of the area of a sphere kind of redundant, since deriving is honestly really easy.
The point I'm trying to get to is that certain things can not be learned by flashcards and other things are way easier and more rewarding to learn without flashcards
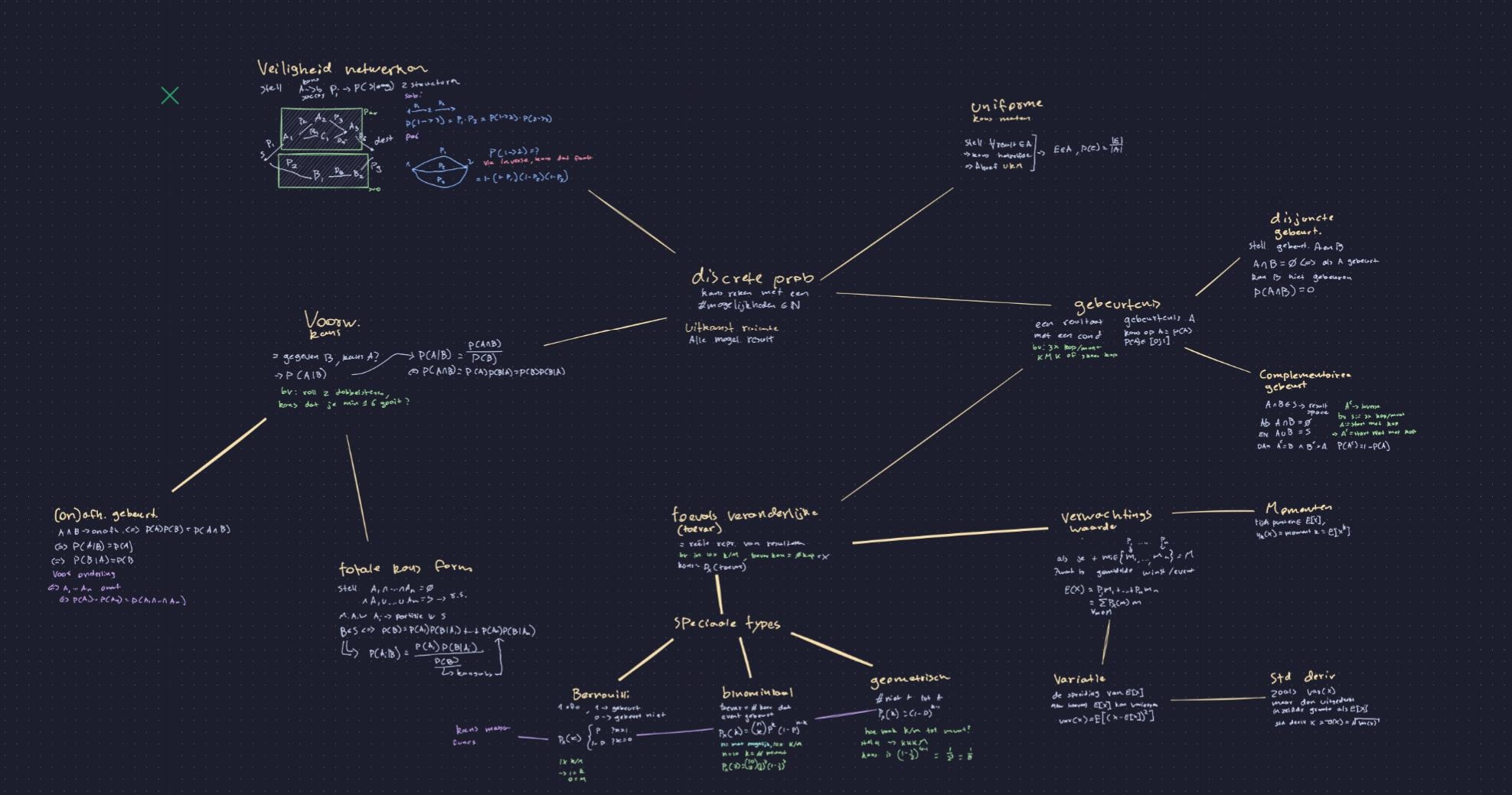
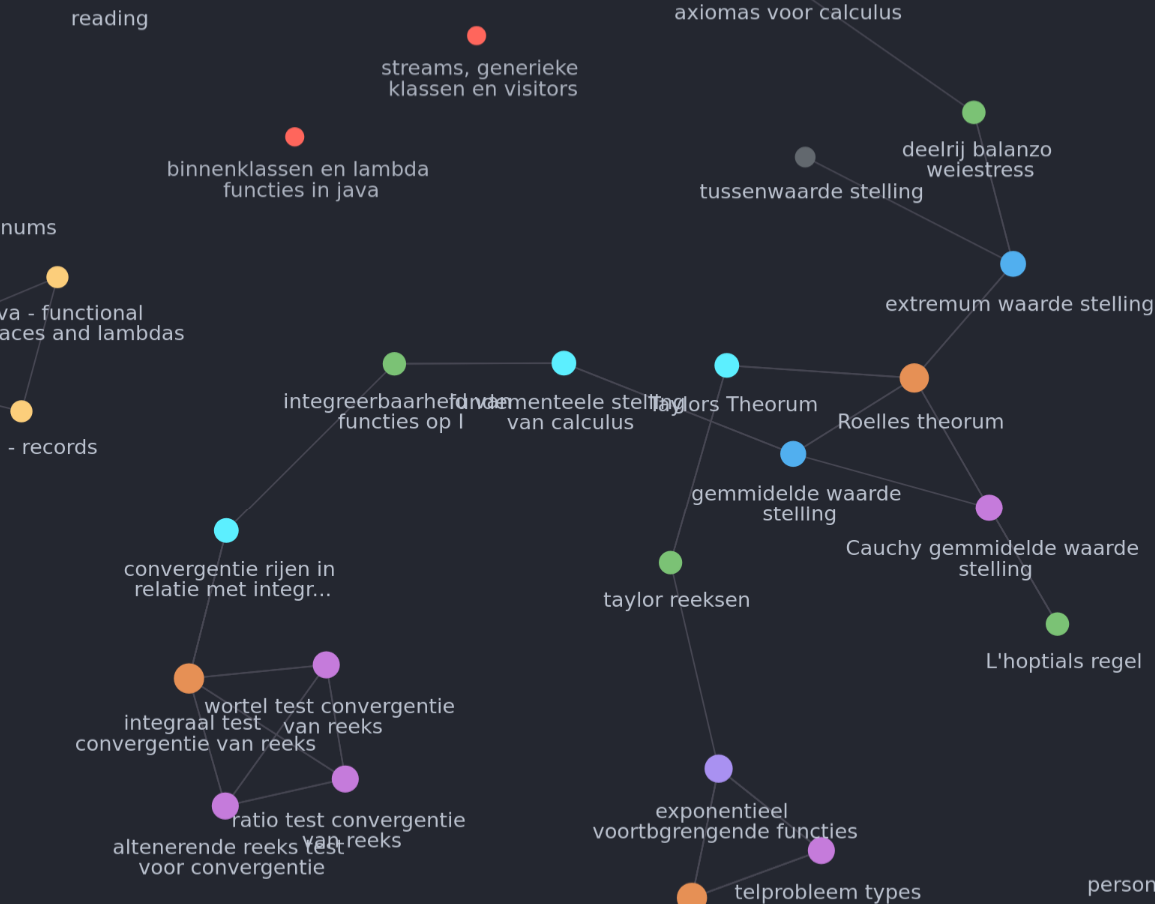
This is a very much a personal preference, but I use mostly non-linear notes. What I mean by this is that I go through a books index, write down keywords that I find, so for example for algorithms and datastructures
Then to finish of I start connection how things relate to eachother, mostly focusing on what i need to know to understand this, so for example for divide and conquer u usually use recursion, recursion is also often used for brute force and branch and bound problems, b&b problems are often represented in trees and trees are usually implemented as arrays.
I do the exact same in plain, all I need is a system that links nodes (and preferably allows me to represent those links via a visual, like for example obsidians graph view). So instead of these keywords being on a page they are just seperate notes, and the description is inside of said note, I usually tend to make these descriptions be more encompasing. For example placing an important math proof in there.